Dies Irae

猛然想起一个名词叫解体报告……

言归正传。

noi2002部分解题报告

Child

题目的意思是有n+m+1个人，其中m个人属于一个组，这个组总是说谎；而n个人属于另一个组，这个组总是说真话，还有1个人是裁判，被问到奇数次的时候说真话而偶数次说谎。可以对每个人询问除他以外的某个人是否属于某个队，但是不能对同一个人问另外的同样一个人的所属问题两次，要求对每个人问不超过2次来确定所有人的组别情况。

我们应该抓住裁判两次回答不同的这个特点来进行考虑，假设说真话的是1（m个），说假话的是0（n个）。
首先，随便选一个人i，问其他人i是否属于某一组（比如0）。如果n!=m，那么可以进行讨论。
1.如果i是裁判，那么就会有n个人说他是0组，而m个人说他不是。
2.如果i是0组的，那么就有m+1个人说他是0组，n-1个人说他不是，其中裁判在那m+1个人里头。
3.如果i是1组的，那么就有n个人说他是0组，m个人说他不是0组，其中裁判在那m个人里头。
   1&3.1.如果m+1和n-1相等，而且恰好出现了相等的数目，那么可以确定i是0的，然后随便抓某个组里头某个人j，问i他是不是0组的。
    1&3.1.1.如果i说是，那么j要么1组要么是裁判(此时是0的，混在1里），然后再在另外一个组里头抓个k问j在的组，k是不是0的，于是会有m个人说是还有一个人说不是。说不是的那个就是裁判，其他是1。
    1&3.1.2.如果i说不是，那么j就是0组的。于是从j在的组里头抓个人k出来给另一个组的人问，问k是不是0，于是会有m个人说是一个人说不是，不是的那个就是裁判，其他是1。
   1&3.2.其他情况，随便抓0组的某个人j，问让m个人的组j是不是0，如果有m个人说是，那么裁判是i，如果有m-1个说是，那么少的那个就是裁判
如果n=m，那么至少我们确定，如果有n-1个人说他不是而m个人说他是，那么他必定是1组的，而且说不是的那n-1个人是0，其余是1。
从某一组中抓个人j出来，问其他人，j是不是1。如果与j同组的人有m-2个答是而有一个答不是，另一个组的都是不是那么就确定了。如果与j同组的人有n-1个答是，另一个组有m-1个答不是而有一个答是，那么j是0。如果与j同组的人有m-1答不是而另外一个组n个人答是，那么j是裁判。这样就讨论完了。
很显然，这样的讨论要求至少每个组的人都不少于2个。小于两个的情形很容易讨论就不再叙述。

dragon
就是说要给一棵带权树的顶点染上m种颜色，其中必须有k个顶点染1号色，而且根节点必须是1号色。其他无限制。统计整棵树上的两个端点颜色相同的边，将这些边的权值求和。求这个和的最小值。
树形DP。首先如果颜色多于2种，那么在染完1号色和2号色之后，总可以找到一种方法交替地染色，使得没有任何一条边端点同色。因此我们只需要考虑两种颜色的情况。
先做一次多叉转二叉，状态是用f[i][j][k]表示i节点为根的子树中需要染j个1号色的最小权和，其中k为0表示i的父亲染1号色，而为1表示染其他颜色。显然题目所求的就是f[0][k][1]。转移就比较明显了，
若i有儿子和兄弟
f[i][j][0] = min( f[child[i]][l][1] + f[brother[i]][j-l][0] , f[child[i]][l][0] + f[brother[i]][j-l-1][0] + w[father[i]][i]); //0<=l<=j或j-1
f[i][j][1] = min( f[child[i]][l][1] + f[brother[i]][j-l][1] + (m>2?0:1) * w[father[i]][i], f[child[i]][l][0] + f[brother[i]][j-l-1][1] ); //0<=l<=j或j-1}
若i有儿子或兄弟
f[i][j][0] = min( f[child[i]或brother[i]][j][1或0], f[child[i]或brother[i]][j-1][0] + w[father[i]][i] )
f[i][j][1] = min( f[child[i]或brother[i]][j][1], f[child[i]或brother[i]][j-1][0或1] + w[father[i]][i] )
若i伶仃孤苦至于成立既无伯叔终鲜兄弟门衰祚薄没有儿息…
f[i][j][0] = (j==1) ? w[father[i]][i] : (j==0?0:inf);
f[i][j][1] = (j==1) ? 0 : (j==0?w[father[i]][i]:inf);
这样就可以了。

galaxy
就是说有许多队列，初始时每个队列i只有一个元素i，要求实现两种操作，第一是把某个队列i的队头接到另一个队列j的队尾，第二是查询某两个元素之间的距离。
这个一看就是并和查，于是想要用并查集（并茶几？）来处理。但是并查集里头的元素都是对等的，无法保存先后顺序。于是我们可以对它进行改进。维护一个数组d，d[i]表示i到i的父亲的距离。每次合并时只需简单赋值，路径压缩和查找时从某个节点开始，一直查找到他的最上层根节点，将路上的距离累加，并一路更新经过的节点。这样查询的时候只需要查询两个元素到根的距离，然后求差就可以了。

day2
这一整套的数学题阿……

robot这题数学味道太浓，至今不能理解。

savage
首先看到这个不大的M（才10^6嘛）就想到要枚举阿枚举。完了之后就是知道m判断是否可行的问题了。对于任意两个野人i和j，假设他们经过x年第一次相遇，于是就要满足 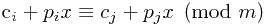 ，其中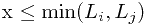。整理一下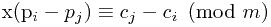，，化成不定方程就是  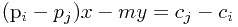。于是就是利用拓展欧几里得来求解。
但是这个题目需要十分注意细节问题。首先是符号，一般书上或者网上给出的拓展欧几里得都是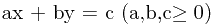的，如果abc的符号不同那就会有不同的结果。而且还要处理如果abc里头某个或者某几个量是0的情况。另外，拓展欧几里得可以直接解的方程是满足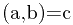的，而有整数解的方程都是满足(a,b)|c的。因此在求解之间必须化简系数。处理完这些之后程序就不短了。
关于符号问题，事实上该题中出现的所有abc的符号情况都可以规约到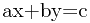与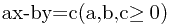的情况，而这两个情况必须分别讨论，后者与前者的区别是一两个符号。下面对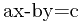的情况进行推导。
显然方程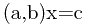的解是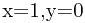。于是假设我们已知方程的解是(x,y)，则方程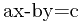的解可以这样得出：

于是