Dies Irae

day1

adv1900

这题是DP优化的经典题。首先，O(nmT)的方程很容易想到。f[i][j][t]表示t时刻在(i,j)时，可以走的最长距离。每一个点有两种选择，用魔法或者不用。由于走的方向已经事先定好了，所以直接推就行了。这个方法可以过60%的点。

考虑这个题的特殊性，T可以很大，k却很小。而且在每个k之中走的方向都是一样的。于是我们可以这么考虑，f[k][i][j]表示在第k时段里头，走到(i,j)时可以达到的最长距离。很显然，f[k][i][j]来自于f[k-1][i-x*di[k]][j-x*dj[k]]，即按照k的方向往回走的某个格子。因为在每个时段里头它都只能往一个方向走，我们可以按照方向把行列分开来处理。比如当前时段只能往北走，那么我们可以把每一列单独拿出来考虑，因为在这个时段之内当前列走不到其他列。假设对于第i列，g[j]表示第i列上从起点开始算起的第j个格子可以得到的最大值。这个起点是指逆着当前方向走，能走到的最远点。比如如果只能往北走，那么起点就是最南点。只有这样推才能满足无后效性，因为从起点开始的每个格子都回不到它前面的那个格子。于是g[j]=max(g[k]+(j-k)) 其中j>k , j-k<=time，time为当前时段的长度。其实这个式子我也想到了，但是直接用这个式子还是无法达到优化的效果。用这个式子来求算，状态是O(nk)，转移是O(n^2)（这里n,m就不区分了，因为不知道具体每个时段走的方向）。最坏情况下还是有可能达到40000*200*200的计算量的（当然，据说直接用这个式子有80%的分）。

对这个式子进行变形，g[j]-j=max(g[k]-k)，用a[j]表示g[j]-j，这样a[j]=max(a[k])，其中j-k<=time。如果把a看成一个数列，那么其实就是在求从j-1开始，长度为time的一段里头的最大值，RMQ啊！于是冲动一下，写个ST或者线段树，或者更有才有闲空地写一个O(n)-O(1)RMQ，唔，那真是天牛了。来仔细分析一下这个查询的特殊性：每次查询长度相同，而且是连续的段。这样可以维护一个单调队列，这个队列可以两边删除，一边插入。我们保持队列从队首向队尾递减。队列中每个元素不仅要存相应的a值，还要有一个时间戳，每当有新的查询时，先把队首过时的元素都删掉，然后返回队首元素，插入时把处在队尾的比新元素小的数全都删掉，然后插入新元素。为什么可以这样做呢？可以这么想，对于每个RMQ问题，如果插入的元素比现在序列里头的某些元素要大，那么那些元素永远不会成为RMQ问题的答案，因为已经有人比他们大而且比他们新了，能够查询到他们的时候也一定能查询到那个新元素，因此没有必要再保存他们了。这样写起来也好写，复杂度是O(n)的，于是总体复杂度降为O(nmk)。

sequence

这个显然是块状链表。因为实在没什么其他的结构能支持那个Reverse命令。对于每一块记录一个量f，标记当前块的读取顺序，即是否reverse。如果reverse的区间恰好处在某块之间，那么就直接swap吧，复杂度不会很大的。最恶心的是max_sum，我想了个无比麻烦的方法，一看报告居然说只要O(n)直接统计就行了，我晕，要是有M/2个max_sum再插了4*10^6个数，看看O(n)的统计还行不行｜｜｜

我想的那个无比麻烦的方法大概是这样，就说把整个序列看成一个数组，那么类似O(n)统计的方法，可以在整个数组中划出许多个分割点，这些分割点表示统计的过程中在这个点时s<0。
例如序列1 2 -4 3 -6 5 9 -10，就应该这么分割：1 2 | -4 | 3 | -6 | 5 9 10 |。这些分割点的个数最多会有n个，如果数组全部都是负数的话。然后在每个操作的时候顺便维护一下这些分割点，比如insert的时候，就需要重新统计最靠近insert点的上一个分割点到下一个分割点之间的段，delete的时候，delete之后就需要重新统计最近的两个分割点之间的状况。特别地，如果delete掉的东西和不为正，就需要重新统计到下一个分割点。reverse的时候只会影响起点和终点所在的地方的分割点，等等。统计的时候可以直接利用每一块的和这个东西。嘛，貌似看起来复杂度也不低，而且把本来复杂度低的操作复杂度也弄高了，于是也不太好。

zhzyx

搜吧。反正我没搜出来，据称裸搜可以有80%。我也不知道为什么，嗯，暴力是美的，嗯。

day2

这套题是这么多NOI题里头我做得最差的，几乎一题也没做出来。

cchkk

这是个DP题，然后我没想出来，然后看了报告好像还不是很明白，听别人说这题巨简单，我也不知道为啥我想不出来，嗯。

首先，从状态来说，只要知道图，以及cc和kk的位置，那么这个概率就确定了。因此只需要用f[i][j]表示cc在i，kk在j时的概率即可。然后推的时候，由于cc一个时间里头可以走两步，而且是cc是一定走了两步之后kk才能走一步。注意，虽然题目中说cc是在没有捉到kk的情况下才走第二步，但我们可以统一处理，如果捉到了cc，就相当于在原地再走一步。首先预处理出一个数组p[i][j]，表示从i走向j时，迈出的第一步。因为题目中说了如果有多条路径一定走编号最小的，所以一定可以在图中找到一棵最短路树，所以就可以用一串连续的p数组序列来表示一条路径。比如i到j的路径可以表示为先走i，然后到p[i][j]，然后到p[p[i][j]][j]，然后到p[p[p[i][j]][j]][j]，……，直到p[...][j]=j为止。当然，为了统一处理两步和一步，我们规定p[i][i]=i。于是方程就可以这么表示

里头第一项表示kk不走，t表示j点的邻接点数目，w[j][k]表示j的第k个邻接点。最后要加1是步数。

很显然，这个方程如果直接推写起来会很麻烦（因为不知道访问顺序），最好的方法是记忆化搜索，效果不错还实惠。

party

略微说一下，1~3是最大生成树，4~6是最小度限制生成树，7~10是乱搞。其实4~6也可以乱搞，反正那算法不麻烦也不简单。

lemon

下面所说的“XX角“，都是XX与水平面的夹角。首先，圆台的影子有两种情况，如果光线角大于母线角，那么影子是一个圆（不是椭圆哦），否则是一个…很怪异的图形，一个梯形，上底和下底分别是个弓形。其实就是圆台的上圆和下圆分别投影之后，作公切线得到的图形封闭部分的面积（图中黄色）。第二，圆锥的影子也有两种情况，光线角大于母线角时是一个圆，否则把顶点投影下去，得到一个三角形去掉一个弓形的部分。（红色）

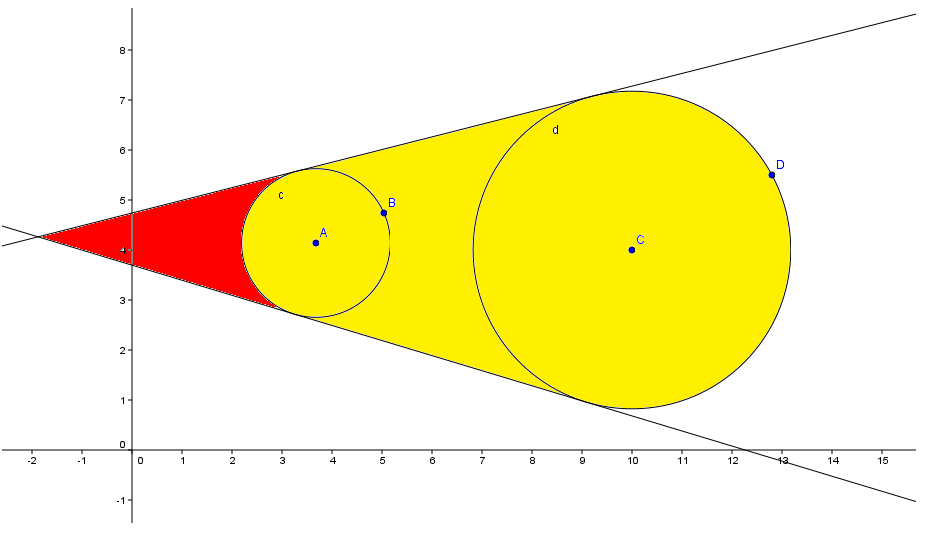
这样，剩下的事情就是求并了。我要求不高，能拿个n=1的分就不错了。