Editor终于AC了,不过不是用块状链表
2008年7月23日 06:57
块状链表实在难写,反正没一次写对的,于是我用Treap来Cheat呵呵,其实Treap的话呢,插入删除和打印操作都是O(nlogL)(n:操作数的长度,L:总长度)的,比起块状链表华丽丽的O(sqrt(n))来啊那可是大大的不美,所以在时间上的差距也很明显(6倍啊OTZ),不过还是AC了,嗯。话说Treap比起朴素的数组实现来说,最大的优势在于LogL上。如果把LogL看成是常数,那么这个插入删除的总复杂度几乎可以看成是O(L)的,其实还是很好的,因为单单把数据读进去就要O(L)的复杂度。朴素的实现,插入或删除是O(n+L)的,积累起来最坏O(L^2),而Treap来说最坏情况期望是O(LlogL),虽然很Cheat,不过还是很有内涵的Cheat。
最近写Treap写得越来越顺手,估计真正比赛的时候如果遇上Treap的题应该也能写对。
从思想上来说呢,把序列存在Treap里头确实不太自然。其实很简单,只要把序列想象成一个个离散的元素加上一个位置标号,然后按照位置标号排序得到的有序队列就可以了。然后按照那个位置标号建立平衡树,就能在平衡树上实现串的操作了。
于是把程序和时间比较贴出来,asdf是HQM的标程。
开始测试 asdf
正在编译 asdf.editor ...成功
正在测试 asdf.editor.0(editor0.in)... 正确 0.308秒 得分: 10
正在测试 asdf.editor.1(editor1.in)... 正确 0.003秒 得分: 10
正在测试 asdf.editor.2(editor2.in)... 正确 0.072秒 得分: 10
正在测试 asdf.editor.3(editor3.in)... 正确 0.085秒 得分: 10
正在测试 asdf.editor.4(editor4.in)... 正确 0.085秒 得分: 10
正在测试 asdf.editor.5(editor5.in)... 正确 0.047秒 得分: 10
正在测试 asdf.editor.6(editor6.in)... 正确 0.053秒 得分: 10
正在测试 asdf.editor.7(editor7.in)... 正确 0.050秒 得分: 10
正在测试 asdf.editor.8(editor8.in)... 正确 0.138秒 得分: 10
正在测试 asdf.editor.9(editor9.in)... 正确 0.258秒 得分: 10
asdf.editor 的总分: 100
asdf 的总分: 100
开始测试 ti
正在编译 ti.editor ...成功
正在测试 ti.editor.0(editor0.in)... 正确 1.771秒 得分: 10
正在测试 ti.editor.1(editor1.in)... 正确 0.003秒 得分: 10
正在测试 ti.editor.2(editor2.in)... 正确 0.663秒 得分: 10
正在测试 ti.editor.3(editor3.in)... 正确 0.743秒 得分: 10
正在测试 ti.editor.4(editor4.in)... 正确 0.734秒 得分: 10
正在测试 ti.editor.5(editor5.in)... 正确 0.524秒 得分: 10
正在测试 ti.editor.6(editor6.in)... 正确 0.526秒 得分: 10
正在测试 ti.editor.7(editor7.in)... 正确 0.518秒 得分: 10
正在测试 ti.editor.8(editor8.in)... 正确 0.668秒 得分: 10
正在测试 ti.editor.9(editor9.in)... 正确 0.920秒 得分: 10
ti.editor 的总分: 100
ti 的总分: 100
#include <cstdlib>
#include <cstring>
FILE *in =fopen("editor.in", "r");
FILE *out =fopen("editor.out", "w");
typedef struct node
{
int k, size;
char ch;
node *l, *r;
} node;
node *t, *nul;
int cursor=1;
node *Right_Rotate(node *t)
{
t->l->size=t->size;
t->size=t->l->r->size+1+t->r->size;
node *t2=t->l;
t->l=t2->r;
t2->r=t;
t=t2;
return t;
}
node *Left_Rotate(node *t)
{
t->r->size=t->size;
t->size=t->r->l->size+1+t->l->size;
node *t2=t->r;
t->r=t2->l;
t2->l=t;
t=t2;
return t;
}
node *Insert2(node *t, int num, char ch)
{
if (t==nul)
{
t=(node*) malloc(sizeof(node));
t->l=t->r=nul;
t->k=rand();
t->ch=ch;
t->size=1;
return t;
}
else
{
t->size++;
t->r=Insert2(t->r, num, ch);
if (t->r->k>t->k) t=Left_Rotate(t);
return t;
}
}
node *Insert(node *t, int num, char ch)
{
if (t==nul) return Insert2(t, num, ch);
if (t->l->size>=num)
{
t->size++;
t->l=Insert(t->l, num, ch);
if (t->l->k>t->k) t = Right_Rotate(t);
return t;
}
else
if (t->l->size+1<num)
{
t->size++;
t->r=Insert(t->r, num-t->l->size-1, ch);
if (t->r->k>t->k) t=Left_Rotate(t);
return t;
}
else
{
t->size++;
t->l=Insert2(t->l, num, ch);
return t;
}
}
node *Delete(node *t)
{
if (t->l==t->r&&t->r==nul)
{
free(t);
return nul;
}
else
if (t->l->k>t->r->k)
{
t->size--;
t=Right_Rotate(t);
t->r=Delete(t->r);
return t;
}
else
{
t->size--;
t=Left_Rotate(t);
t->l=Delete(t->l);
return t;
}
}
void Clear(node *t)
{
if (t==nul) return;
Clear(t->l);
Clear(t->r);
free(t);
}
node *Delete(node *t, int st, int ed)
{
if (st>ed) return t;
if (t->l->size+1<st)
{
t->size-=(ed-st+1);
t->r=Delete(t->r, st-(t->l->size+1), ed-(t->l->size+1));
return t;
}
else
if (t->l->size+1==st)
{
t=Delete(t);
return Delete(t, st, ed-1);
}
else
if (st==1&&ed==t->size)
{
Clear(t);
return nul;
}
else
if (ed<=t->l->size)
{
t->size-=ed-st+1;
t->l=Delete(t->l, st, ed);
return t;
}
else
{
t->size-=ed-st;
int l=t->l->size-st+1;
t->l=Delete(t->l, st, t->l->size);
t->r=Delete(t->r, 1, (ed-st+1)-l-1);
t=Delete(t);
return t;
}
}
void Print(node *t, int st, int ed)
{
if (st>ed) return;
if (t==nul) return;
if (st>t->l->size+1) Print(t->r, st-(t->l->size+1), ed-(t->l->size+1));
else
if (st==t->l->size+1)
{
fprintf(out, "%c", t->ch);
Print(t->r, 1, ed-st);
}
else
if (ed<=t->l->size) Print(t->l, st, ed);
else
if (ed==t->l->size+1)
{
Print(t->l, st, ed-1);
fprintf(out, "%c", t->ch);
}
else
{
Print(t->l, st, t->l->size);
fprintf(out, "%c", t->ch);
Print(t->r, 1, (ed-st+1)-(t->l->size-st+1)-1);
}
}
int main()
{
int lines;
fscanf(in, "%d\n", &lines);
nul = (node*) malloc(sizeof(node));
nul->l=nul->r=nul;
nul->k=-RAND_MAX;
nul->ch=0;
nul->size=0;
t=nul;
//initialize
for (int i=0;i<lines;i++)
{
char ch,ch2;
int num;
char s1[200];
ch=fgetc(in);
ch2=fgetc(in);
while (ch2!='\n'&&ch2!=' ') ch2=fgetc(in);
if (ch!='P'&&ch!='N') fscanf(in, "%d", &num);
if (ch2!='\n') fgetc(in);
switch (ch)
{
case 'M':
cursor=num+1;
break;
case 'I':
for (int j=0;j<num;j++)
{
char ch3;
ch3=fgetc(in);
while (ch3=='\n') ch3=fgetc(in);
t=Insert(t, cursor+j, ch3);
}
fgetc(in);
break;
case 'D':
t=Delete(t, cursor, cursor+num-1);
break;
case 'G':
Print(t, cursor, cursor+num-1);
fprintf(out, "\n");
break;
case 'P':
cursor--;
break;
case 'N':
cursor++;
break;
}
}
}

![\[ \begin{bmatrix} 2&-1&-1& 0& 0\\-1& 3&-1&-1& 0\\ -1&-1& 4&-1&-1\\ 0&-1&-1& 4&-1\\ 0& 0&-1&-1& 3\\ \end{bmatrix} \] \[ \begin{bmatrix} 2&-1&-1& 0& 0\\-1& 3&-1&-1& 0\\ -1&-1& 4&-1&-1\\ 0&-1&-1& 4&-1\\ 0& 0&-1&-1& 3\\ \end{bmatrix} \]](http://agnimon.is-programmer.com/user_files/agnimon/epics/cbe910750b6838a38c838d15309efe97c5419fe9.png)
![\[ f[i][l][S] = \min_{0 \le k \le l} { f[child[i][0]][k][S+newS] + f[child[i][1]][l-k][S+newS] } \] \[ f[i][l][S] = \min_{0 \le k \le l} { f[child[i][0]][k][S+newS] + f[child[i][1]][l-k][S+newS] } \]](http://agnimon.is-programmer.com/user_files/agnimon/epics/58200a269d337447cd272342034c7c5900e28a2b.png)
![\[s=\sum_{i=1}^t a[i]\] \[s=\sum_{i=1}^t a[i]\]](http://agnimon.is-programmer.com/user_files/agnimon/epics/18e6ad6667b1d3d8b66e353f67f47db67e74822a.png) ,那么
,那么![\[ \begin{matrix} P & = &\sum_{1 \le i \le t, i \ne k} \frac{a[i]}{s} \times \frac{a[k]}{s+d} + \frac{a[k]}{s} \times \frac{a[k]+d}{s+d} \\ \ & = & \frac{s-a[k]}{s} \times \frac{a[k]}{s+d} + \frac{a[k]}{s} \times \frac{a[k]+d}{s+d} \\ \ & = & \frac{sa[k] - (a[k])^2 + (a[k])^2 + a[k]d}{s(s+d)} \\ \ &=& \frac{a[k]}{s} \end{matrix} \] \[ \begin{matrix} P & = &\sum_{1 \le i \le t, i \ne k} \frac{a[i]}{s} \times \frac{a[k]}{s+d} + \frac{a[k]}{s} \times \frac{a[k]+d}{s+d} \\ \ & = & \frac{s-a[k]}{s} \times \frac{a[k]}{s+d} + \frac{a[k]}{s} \times \frac{a[k]+d}{s+d} \\ \ & = & \frac{sa[k] - (a[k])^2 + (a[k])^2 + a[k]d}{s(s+d)} \\ \ &=& \frac{a[k]}{s} \end{matrix} \]](http://agnimon.is-programmer.com/user_files/agnimon/epics/67bdc40334ac89c7933926dd25b989af2032435f.png)
![\begin{displaymath} f[i][j]= \frac { f[p[p[i][j]][j]][j] + \sum_{k=0}^t f[p[p[i][j]][j]][w[j][k]] } {t+1} + 1 \end{displaymath} \begin{displaymath} f[i][j]= \frac { f[p[p[i][j]][j]][j] + \sum_{k=0}^t f[p[p[i][j]][j]][w[j][k]] } {t+1} + 1 \end{displaymath}](/user_files/agnimon/epics/18d2886bd1cc05c076a36f0b5f347be3b9fdc61f.png)
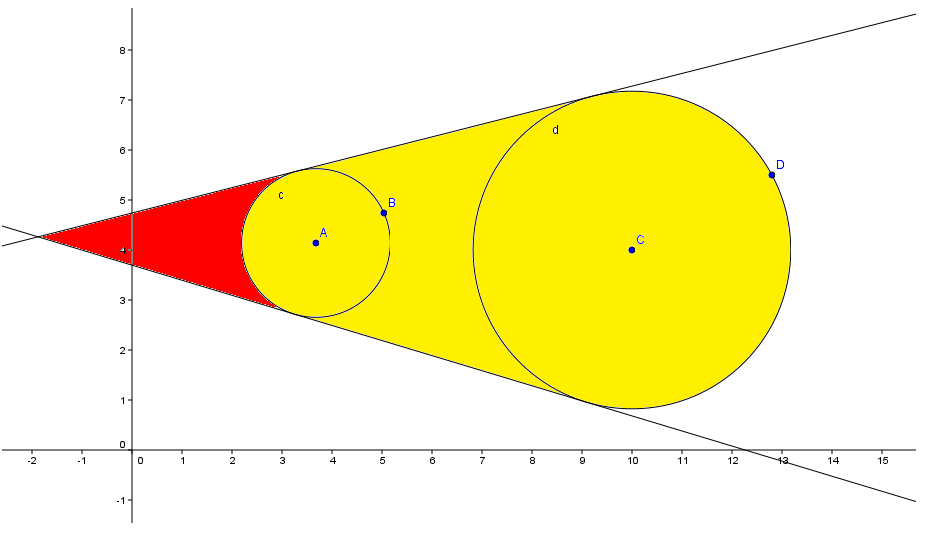

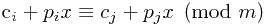 ,其中
,其中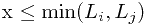 。整理一下,
。整理一下,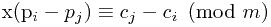 ,化成不定方程就是
,化成不定方程就是 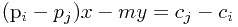 。于是就是利用拓展欧几里得来求解。
。于是就是利用拓展欧几里得来求解。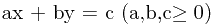 的,如果abc的符号不同那就会有不同的结果。而且还要处理如果abc里头某个或者某几个量是0的情况。另外,拓展欧几里得可以直接解的方程是满足
的,如果abc的符号不同那就会有不同的结果。而且还要处理如果abc里头某个或者某几个量是0的情况。另外,拓展欧几里得可以直接解的方程是满足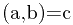 的,而有整数解的方程都是满足(a,b)|c的。因此在求解之间必须化简系数。处理完这些之后程序就不短了。
的,而有整数解的方程都是满足(a,b)|c的。因此在求解之间必须化简系数。处理完这些之后程序就不短了。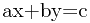 与
与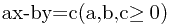 的情况,而这两个情况必须分别讨论,后者与前者的区别是一两个符号。下面对
的情况,而这两个情况必须分别讨论,后者与前者的区别是一两个符号。下面对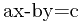 的情况进行推导。
的情况进行推导。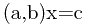 的解是
的解是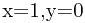 。于是假设我们已知方程
。于是假设我们已知方程 的解是(x,y),则方程
的解是(x,y),则方程![\[\begin{matrix} bx - (a \bmod b)y & = &bx - \left ( a - \left \lfloor \frac{a}{b} \right \rfloor \times b \right ) y \\ \ &=& a(-y) - b(-x-\left \lfloor \frac{a}{b} \right \rfloor \times y) \end{matrix} \] \[\begin{matrix} bx - (a \bmod b)y & = &bx - \left ( a - \left \lfloor \frac{a}{b} \right \rfloor \times b \right ) y \\ \ &=& a(-y) - b(-x-\left \lfloor \frac{a}{b} \right \rfloor \times y) \end{matrix} \]](/user_files/agnimon/epics/a8b6a4e861147318185d43ac947eaf7e528d82ce.png)
![\[\begin{matrix} x^\prime&=&-y \\ y^\prime&=&-x-\left \lfloor \frac{a}{b} \right \rfloor \times y\end{matrix}\] \[\begin{matrix} x^\prime&=&-y \\ y^\prime&=&-x-\left \lfloor \frac{a}{b} \right \rfloor \times y\end{matrix}\]](/user_files/agnimon/epics/aa3d57082eb5ba9927556953b07204b2416af9cf.png)