NOI2004解题报告

day1
cashier
对一个数列，完成四种操作。所有元素增加或减少一个给定量，向数列中插入某个元素，查询数列中第k大元素。另外，在任何操作之后，数列中所有小于某个值的量都会被删除，这个数目也要统计。

这题我用treap和树状数组分别做了一次。我手头的数据是错的，反正我拿标程和我的两个程序对，答案都一样，而且和数据里头的答案的查询结果一样，就是删除的数目不同，而且差很多。于是就认为是答案错了。｜｜

treap和树状数组的思想是不同的，但是有一个处理是一样的：因为增加的操作不会影响数据的相互关系，减少和插入操作才有可能影响，所以我们需要一个改变量delta，当增加时就直接增加delta，减少时不仅减少delta还要处理删除元素，插入时要把插入的量减去一个delta。

Treap保存的是元素，增加一个size域用于查询，增加一个delta域表示这棵子树的值都需要加上delta，还有一个num域处理重复节点。然后增加的时候在根节点的delta上处理。关于delta的的操作就像线段树的lazy操作一样，当访问到某个节点的时候就把根的值加上delta，然后把delta加到左右儿子的delta上，然后把根的改成0，这叫做delta的传递。插入和查询的时候都可以顺便传递delta，节约时间。因为删除的时候是整个整个地删，所以操作的时候也不用费心去调整了，直接free掉了事。这样就可以了。写treap的时候有些地方要注意，就是rotate的时候千万不要忘记更新域，有些域在rotate下是不变的，比如这里的delta和num，但最常用的size域是会变的，千万不要忘了更新。

树状数组第i个节点保存的是值小于i-1的元素有多少个（当然实际数组的值肯定不是这个）。由于可能出现0，而树状数组下标必须从1开始，所以要用i-1。要保存一个curmax和curmin，表示当前在树状数组中的数的最小值和最大值。然后那个delta表示整个数组的偏移量，每次插入的时候如果插入的值减掉delta还是正数的话就直接插，否则就要把数组平移delta，以保证插入的元素是正数。平移的时候不能简单地move，因为下标是和保存的值有关的，所以干脆就直接枚举每个元素（也就是从curmin到curmax），加上delta然后插入一个新的数组里头。于是这里就成了程序的瓶颈，虽然复杂度很不小，但是次数貌似不算多，所以实际效果很好。然后删除的时候就相当于给小于它的每个元素减掉该元素的数量，这儿也要枚举元素，不过只需要从min到curmin就可以了。我感觉我这方法复杂度应该不低，但是实际效果居然比treap好很多，真神奇…

manhattan

这曼哈顿做的我头昏脑胀，到了最后居然被lowsars给误删了｜｜｜｜｜｜｜｜｜｜｜｜太郁闷了｜｜｜｜｜｜｜于是就不打算重写了，管他对不对｜｜｜｜
其实这个题的方法我想到了一半，另一半我打算用图论算法实现，然后想破脑袋也没想出来，一看题解原来是DP…我没想到可以用区间表示，所以想不到DP…T_T

首先，这个那么小的m一看就勾引人去枚举…然后任何两点的manhattan路径都可以规约成以下四种情况。

也就是说枚举了m然后我们只需要找到一个合法的n方向的方案满足所有要求就行了。然后我想到这一步就总是在想这些约束关系可以离散成许多个用与或关联词连接的约束，然后以约束为顶点，设法构图把这些关联词表达出来，想了一个早上也没想出来｜｜其实关键问题是在或关联词上，与关联词是很容易表达的，而且有些约束是要两个点有些是一个，虽然后来想出了一个方法可以把两个的和一个的统一起来表示，但是在那个表示方法下与或关联词都很不好表达。所以很WS地看题解去了。原来题解是把这些约束用区间来表示，[s,t](r)表示在n方向上的[s,t]区间里头，至少要有一条边方向是r。然后这四种情况就可以很方便地表示为许多个只有与关联词的约束关系。这是个突破口。如果只有与关联词那就好办了，首先把区间分类，有些是方向0的有些是要1的，分开处理，将具有包含关系的区间中删大的留小的，因为小的区间满足了大的自然也就满足了。对区间左端点排序，左端点相等的按右端点排序，然后DP，f[i][j][k]表示扫描线在i的时候0区间可以满足的最后一个为j，1区间可以满足的最后一个叫k，状态表示也不太好想到，反正我是没想到。想到了这个状态表示之后转移就很容易了。假设l表示左端点大于i+1的第一个0或1区间编号，那么f[i][j][k]就应该转移到f[i+1][l-1][k]（即y是方向0）或者f[i+1][j][l-1]（y是方向1）。

dune

这题不会做，看amber的报告吧

day2

hut

这个题可以DP也可以贪心，我不知道为什么老是调不过那个DP，于是就写了贪心的。DP的想法很简单，f[i][j][k]表示x位置在i，对应的南墙有j个块，北墙有k个块。于是推起来就很明显了，f[i-x][j-y][k-1]。就相当于枚举最后一块北墙的长度x，再这个x对应的南墙墙数y。很显然这y块都必须尽量平均。但是这样复杂度比较高，是O(L^2N^2M)，无法接受。注意到北墙块实际上是没有顺序的（交换之后对应的南墙块也要交换），也就是说可以任意交换而不改变结果。于是我们使北墙块的长度递增，长度相等时按照南墙块数目排序。这样我们发现，当确定x之后，枚举y的过程实际上是单峰型的，也就是存在且仅存在一个极值，那么这个极值（假设是y）必定满足y-1和y+1都不小于它，找到了这样的点就可以认定它是极值点了。确定了当前x对应的y之后，让x++，此时块数必定不比y少（因为要平均），因此直接从y开始枚举就可以了。这样，转移的复杂度从O(LN)变成了O(L)，总复杂度也就变成了O(L^2NM)，这是可以接受的。问题是这个DP我怎么调都调不过，然后看了amber的报告就按照他那个贪心来写了。

贪心的方法是基于平均分配的思想。考虑到南墙有m块，北墙有n块，最好的情况当然是每块北墙都分到m/n块南墙（因为最平均嘛），但是如果m不能被n整除呢？那就首先尽量平均，然后多出来的部分再平均地放在某些块里头。也就是说北墙对应南墙有两种，一种是拿到[m/n]块，另一种拿到[m/n+1]块。正如刚才所说，北墙的顺序是无关紧要的，于是我们把北墙按种类排序，也就是找到一个分点i，使得i的左边的所有北墙都是[m/n]型的，而右边所有的都是[m/n]+1型的。然后再考虑长度，如果每块北墙（或者南墙）分不到恰好整数的长度，也是一样，先尽量平均，然后再把多出来的再平均放。于是复杂度就是O(L)，我是直接合并写成了一个式子，虽然看起来比较难看，不过思想还是很明显的。

rainfall

这个题其实是几何题，只不过需要一些转化。首先，我们用s-t图线表示所有自动伞的运动。每一个自动伞可以看成两个端点之内的部分，也就是图中着色了的部分。每一种颜色代表一个伞。这样，我们要求的降雨面积其实就是总面积减掉伞面积。（下面图片是大图，不过貌似在firefox里头会自动缩小，然后就看不太清楚了，可以点开来看）

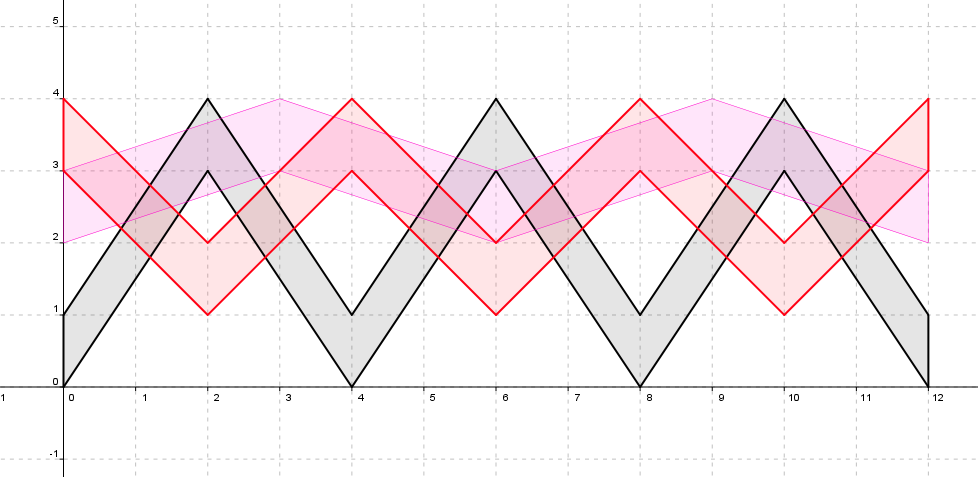
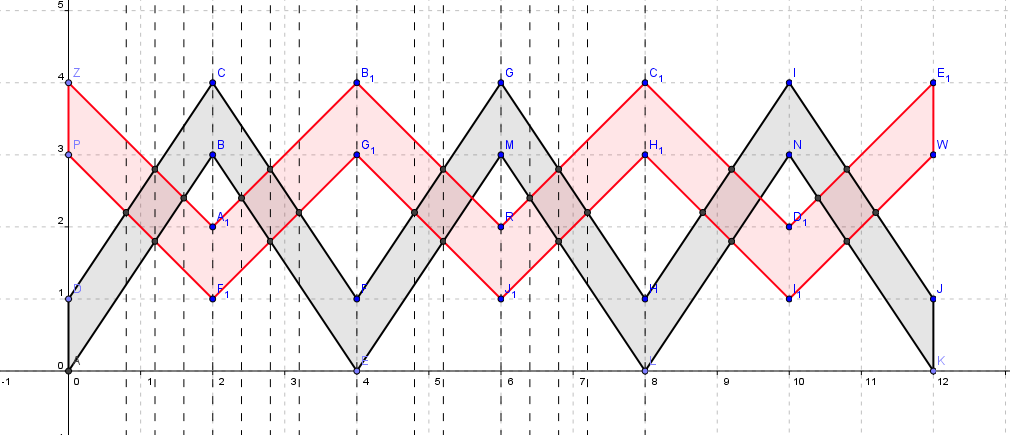
我们按交点和拐点对整个图形离散化（图中只是表示出了两个伞的情况）。这样我们就发现任何两个事件点之间的图形其实就是许多平行四边形的并。再仔细看每一根虚线上的点，其实两个事件点i和i+1之间的面积可以用l_i（在第i条直线上的线段长度之和）与l_{i+1}求出，具体地，S=(l_i+l_i+1)*(x_{i+1}-x_i)/2。这就是梯形面积。于是问题就解决了。