Dies Irae

day1

network

任意两点间最短路径的数目可以在floyd的基础上加一点东西来计算。floyd中，如果满足f[i][j]>f[i][k]+f[k][j]，那么把g[i][j]更新为g[i][k]*g[k][j]，如果f[i][j]==f[i][k]+f[k][j]，那么g[i][j]+=g[i][k]*g[k][j]。然后经过v的最短路径的数目可以枚举s顶点和t顶点，如果满足f[s][v]+f[v][t]=f[s][t]，那么路径数目增加g[s][v]*g[v][t]。这样就解决了。帅哥周源的那个题解提供的第三个方法没去看，对这题n^3足矣。他那个是NM的，适用于稀疏图。

cash

cash这题啊，我的能力也就只能拿60分了。方程是很显然的，f[i]=max(f[i-1], f[j]+w[j][i])。f里头存的都是人民币，w[j][i]表示在第j天用所有钱买入，然后到第i天卖出。这是n^2的。标程是nlogn的，那解法实在太神奇，是用treap优化的dp，于是我觉得我想得到也写不出啊orz。

day2

necklace

这题是个比较简单的数据结构题。不过是个线段树而已，而且居然开了4s，也算是好RP了。估计数组模拟都可以过不少吧。需要注意的是，rotate和flip并不改变珠子之间的相对顺序，所以就用个标记搞定就可以了。
然而这个也没有一次AC，是在rotate的时候一个head-=n手误成了head+=n，其实是原来改过的，后来忘了改回去了。

count

我估计我能在比赛的时候写的方法是消元。首先，算行列式的时候我们可以利用矩阵初等变换把它消成三角阵，然后把对角线上的数乘起来，这个值就是原来行列式的值。初等变换是指把某一行乘上某个常数然后加到另一行上，例如：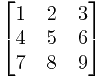
第一行乘上它下面每一行的第一个数的相反数，加到该行上。

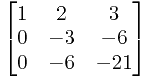
第二行乘上它下面每一行的第一个数的相反数，加到该行上。

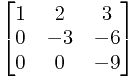
这样，原行列式的值是1*(-3)*(-9)=27。

行列式的值在初等变换下不变。直接做是n^3的，然而这个矩阵是如此特殊，它只有中间那么一块有东西，其他都是0，比如n=6，k=2的情况

很显然，我们没有必要去用一行来消它下面的所有行，因为有很多已经是0了，只需要消它下面k行就可以了。于是我们得到了一个O(n^2k)的算法，据说可以得70~80分，也不错了。

题解上写了DP的方法，不过始终还是很麻烦，虽然效果确实比消元好，相应地思维复杂度也比消元高很多。对于k=2，大概想法是把n顶点的图分成两类，一类是n与n-1直接相连的，一类是n与n-1不直接相连的，这样就可以推了，其他情况也类似，但是k>=4的时候用手是肯定写不出那些情况了的，据说有分别有三十多种、五十多种，所以就要靠一个DFS先确定转移方程上的系数，然后再确定初值，反正无比麻烦就对了。

catch

虽然我没能力完美解决这个题（他那解决的程序可是有8k多呢…还是C的呢，这难道能写得完的么OTZ），不过骗个三四十分还是可以的。而且程序也不算很麻烦，用一个多小时肯定能写完调完了。

想法是这样，首先，因为是树形结构，很自然地想到类似tree-dp的方法：
用tree(i)表示清空i节点。所谓清空，就是通过一些步骤保证他不可能在i以及i的子树中。结束之后，必须在i节点保留且只保留一个人。
对当前节点i，
1.如果度为1，那么这个点显然是叶子，我们设法保证，不会有递归到叶子节点的情况。
2.如果度为2，有两种情况。要么这个点是根，这样就有两个儿子。首先检查儿子是否是叶子，如果是叶子，而且i上没有人，就在左儿子分配一个，然后移动到i，然后再移动到右儿子，然后再返回i。否则用i上的人来移动。要么这个点是某个非叶节点，那么只需要判断儿子是否是叶子，类似地做。
3.如果度大于2，那么首先在i分配一个人，然后再在i分配一个人去扫荡i的儿子中的叶子节点，然后再递归地清空i的非叶儿子。
这个方法是一定满足条件的，不过貌似分配的人多了一点，嘛，得了40分，也算可以了，嗯。

至此，NOI近5年的题解题报告（其实也不能算是解题报告，最多是解题思路…或者甚至是心得这类东西…）就结束了。